安徽数量关系遇方阵别慌，找规律得答案
安徽公务员考试行测数量关系技巧 方阵问题是数量关系中一类常见问题，是许多人或物按一定的条件排成正方形(简称方阵)，再根据排成的方阵，找出规律，寻求解决问题的方案。常见的方阵有实心方阵和空心方阵两种。在解决方阵问题时，首先应该准确判断方阵的类型，要搞清方阵中的一些量(如层数、最外层人数、最里层人数、总人数)之间的关系。再运用相关公式来解题，以下，我们结合理解讲解：
数量关系例题讲解 一、实心方阵
1.模型介绍：
2.规律总结：
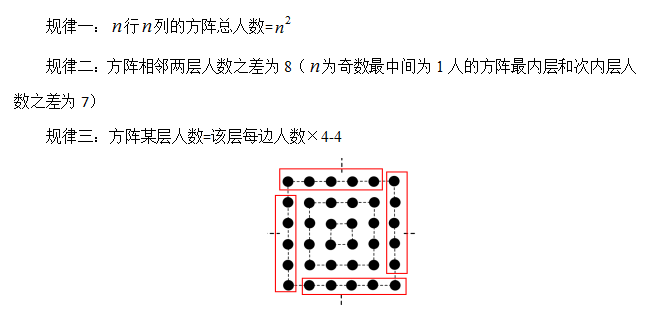
3.例题精讲
例1、某部队的全体官兵刚好排成一个方阵，最外层人数是128人，则该部队共有多少名官兵?
A.529
B.783
C.1089
D.1122
【解析】C。最外层人数为128人，即最外层每边人数×4-4=128，计算可知最外层每边人数=33，故选择C选项。
例2、某高二年级学生组成方阵，已知该方阵从外向里数第二层人数是100人，那么该方阵总人数为( )人。
A.529
B.625
C.729
D.784
【解析】D。方阵从外往里数第二层100人，则最外层人数为108人，即最外层每边人数×4-4=108，计算可知最外层每边人数=28，故选择D选项。
二、空心方阵
1.模型介绍
空心方阵是由实心方阵演变而来，即将实心方阵中间掏去若干层。
正中间有一个人的正方形阵列掏去中间若干层，如下图所示为掏去中间一层，任意一层每边人数n为奇数。
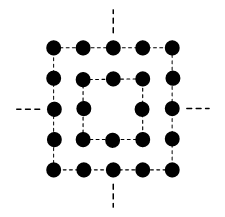
正中间有四个人的正方形阵列掏去中间若干层，如下图所示为掏去中间一层，任意一层每边人数n为偶数。
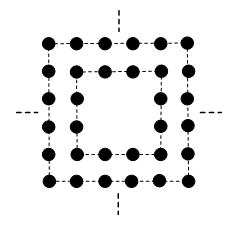
2.规律总结
规律一：方阵相邻两层人数之差为8
规律二：方阵某层人数=该层每边人数×4-4(可理解为正方形的周长=边长×4，拐角处的人均重复计算)
3.例题精讲
例题、小王在装修时，准备在正方形电视墙的外围贴正方形瓷砖，由内到外一层北欧绿色，一层北欧蓝色交替铺，已知共贴了5层，最外层一条边上贴了30块瓷砖，则电视墙的外围共贴了多少块北欧绿色瓷砖?
A.300
B.324
C.416
D.500
【解析】A。五层瓷砖由内向外的颜色依次为北欧绿色、北欧蓝色、北欧绿色、北欧蓝色、北欧绿色，最外层一边的瓷砖数为30，则最外层共贴30×4-4=116块，由外向内所贴瓷砖数量依次为116块、108块、100块、92块、84块，所用北欧绿色瓷砖共116+100+84=300块。故选择A选项。
大家在备考中需要注意的是，在方阵问题中，若题干中没有明确说明是实心方阵还是空心方阵，则默认为实心方阵。
安徽公务员考试备考2024年安徽公务员笔试时间预计在2024年3月，历年来公共笔试科目为《行政职业能力测验》和《申论》，需要备考公共笔试科目的考生可借鉴参考2024年安徽公务员考试用书（点击订购）备考。
点击分享此信息：
相关文章
